In my last post, my students were wrestling with a question about cereal prizes. Namely, if there is one of three (uniformly distributed) prizes in every box, what's the probability that buying three boxes will result in my ending up with all three different prizes? Not so great, turns out. It's only 2/9. Of course this raises another natural question: How many stupid freaking boxes do I have to buy in order to get all three prizes?
There's no answer, really. No number of boxes will mathematically guarantee my success. Just as I can theoretically flip a coin for as long as I'd like without ever getting tails, it's within the realm of possibility that no number of purchases will garner me all three prizes. But, just like the coin, students get the sense that it's extremely unlikely that you'd buy lots and lots of boxes without getting at least one of each prize. And they're right. So let's tweak the question a little: How many boxes do I have to buy on average in order to get all three prizes? That's more doable, at least experimentally.
I have three sections of Advanced Algebra with 25 - 30 students apiece. I gave them all dice to simulate purchases and turned my classroom---for about ten minutes at least---into a mathematical sweatshop churning out Monte Carlo shopping sprees. The average numbers of purchases needed to acquire all prizes were 5.12, 5.00, and 5.42. How good are those estimates?
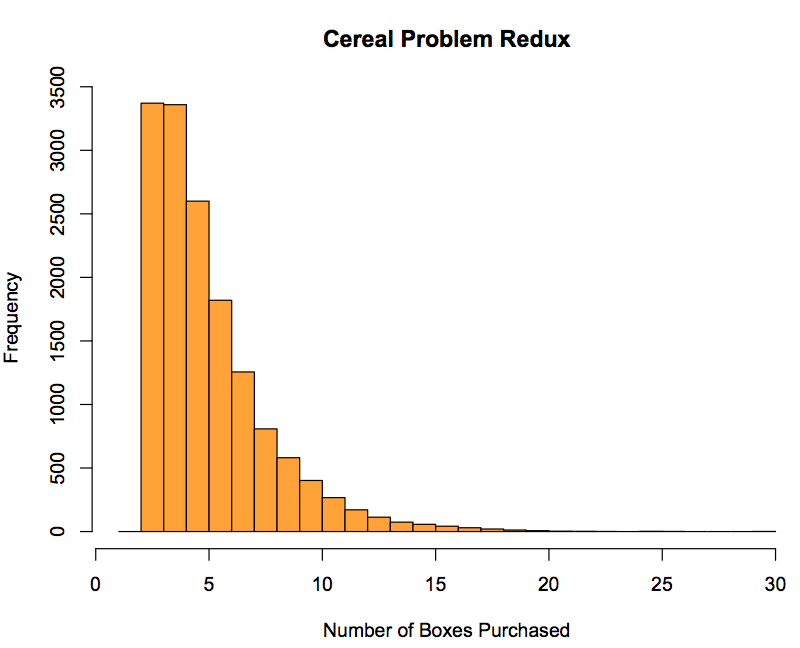
Here's my own simulation of 15,000 trials, generated in Python and plotted in R:
I ended up with a mean of 5.498 purchases, which is impressively close to the theoretical expected value of 5.5. So our little experiment wasn't too bad, especially since I'm positive there was a fair amount of miscounting, and precisely one die that's still MIA from excessively enthusiastic randomization.
And now here's where I'm stuck. I can show my kids the simulation results. They have faith---even though we haven't formally talked about it yet---in the Law of Large Numbers, and this will thoroughly convince them the answer is about 5.5. I can even tell them that the theoretical expected value is exactly 5.5. I can even have them articulate that it will take them precisely one box to get the first new toy, and three boxes, on average, to get the last new toy (since the probability of getting it is 1/3, they feel in their bones that they should have to buy an average of 3 boxes to get it). But I feel like we're still nowhere near justifying that the expected number of boxes for the second toy is 3/2.
For starters, a fair number of kids are still struggling with the idea that the expected value of a random variable doesn't have to be a value that the variable can actually attain. I'm also not sure how to get at this next bit. The absolute certainty of getting a new prize in the first box is self-evident. The idea that, with a probability of success of 1/3, it ought "normally" to take 3 tries to succeed is intuitive. But those just aren't enough data points to lead to the general conjecture (and truth) that, if the probability of success for a Bernoulli trial is p, then the expected number of trials to succeed is 1/p. And that's exactly the fact we need to prove the theoretical solution. Really, that's what we need basically to solve the problem completely for any number of prizes. After that, it's straightforward:
The probability of getting the first new prize is n/n. The probability of getting the second new prize is (n-1)/n ... all the way down until we get the last new prize with probability 1/n. The expected numbers of boxes we need to get all those prizes are just the reciprocals of the probabilities, so we can add them all together...
If X is the number of boxes needed to get all n prizes, then
$latex E(X) = frac{n}{n} + frac{n}{n-1} + cdots + frac{n}{1} = n(frac{1}{n} + frac{1}{n-1} + cdots + frac{1}{1}) = n cdot H_n&s=2$
where Hn is the nth harmonic number. Boom.
Oh, but yeah, I'm stuck.