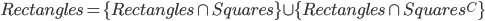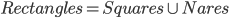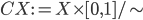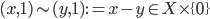In accordance with the 7th Commandment of Blogging (If thy comment exceedeth two cubits in length, thou shalt write thine own damn post.), here is my personal response to Dan's latest question. To be clear: even though the question was put to Mathalicious generally, and even though I bodily occupy a nontrivial fraction of that particular organization, it would be presumptuous of me to write anything approaching an official opinion, especially given the humbling brains attached to the people I spend my days with. But I have thoughts.
We do thump the real-world drum pretty steadily around the office. We have, as it's known in the biz, a niche. But what exactly constitutes 'real-world' is an interesting question. I don't think it's a particularly important question, but it's interesting insofar as it informs the practical decisions I make about what kinds of tasks I try to author, and what kinds of tasks I leave to other smart people, in other well-appointed niches. And insofar as that term appears with some regularity in the CCSS.
A Line in the Sand
There's a philosophically defensible sense in which nothing we'd call a mathematical object is real (or, for that matter, an object). They're abstract and causally independent and yadda yadda yadda. There's another philosophically defensible sense in which everything we'd call a mathematical object is real. Actually, a couple of senses, with varying definitions of reality. And of course there are positions in between. You could spend lifetime trying to untangle all the competing ideas of what (or whether) a number is. And basically who cares. In my mind, there's a simple way to draw a (note: not the) line on the curricular map between That Which Is Real and That Which Is Not:
Is this question self-referential?
In other words, are we using math to examine itself, or are we using it to inspect something outside its own borders? So my working definition of 'real-world' math is a mathematical task that is not self-referential. Which means, and I suppose you saw this coming, that my answer to Dan's question is none of the above. None of those problems is real-world in any appreciable sense. They are all questions about a circle, a square, and their respective areas: math looking at math. A and B are obvious. C and D are just promising hypothetical candy (which is the absolute worst kind of candy) for solving A or B. I suppose E and F are both dipping their toes into the real-world, but self-consciously.
Okay, so those are some counterexamples. Maybe a countercounterexample will help shed light on my litmus test.
For Instance...
Here are two problems:
1. Is it true in general that P(A|B) = P(B|A)? If not, can you express P(A|B) in terms of P(B|A)?
2. Should innocent people be worried about the NSA's PRISM program? How much should they be worried?
By my definition, the second question is 'real-world' and the first one is not, because the first question is mathematically self-referential (it's a question about a mathematical relationship phrased in mathematical language) and the second one is not (it's a question about personal liberty and national security phrased in natural language). Of course they are the same question, and they are both excellent. But from my chair, the very fact that those questions are the same is so non-obvious that connecting them requires a profound act of mathematical thinking. Also, you get to do some really good math qua math. I find that both professionally compelling and pedagogically useful. That's why I do what I do. Without speaking too forcefully for the rest of the team, I think that's part of the reason we do what we do.
Unpacking Circles
As I understand Dan's position (or at least one particular aspect of Dan's position), there's no reason to create a distinction between, e.g., a circle's reality and the reality of health insurance. In fact, for kids, a circle may be real (Platonist objections notwithstanding) in a much clearer and more visceral way. And from there it's not a particularly ambitious leap to extend this reasoning such that all of mathematics can be considered practically real to human beings living in a world that includes mathematics. I think that's about right.
But I also think it's valuable to make just this sort of distinction from time to time. Learning mathematics (or maybe just learning) has a lot to do with forming connections. You can know something about addition. You can know something about subtraction. But when you --- a much younger you --- begin to wrap your head around the connection between the two operations, important things are happening. And a connection's impact on understanding is inversely related to its obviousness. The guy who understands the connection between multiplication and division has learned an important thing. The guy who understands the connection between the zeros of a complex function and the distribution of prime numbers has revolutionized an entire field.
I'm personally interested in helping people make non-obvious connections. There are lots of good ways to do that, and we as educators should pursue all of them, but one way is to connect clearly mathematical ideas to questions that are not clearly mathematical in scope, viz., ask real-world (as I've defined it) questions.
Silver Bullet
So essentially my job boils down to finding interesting non-mathematical questions that are isomorphic to interesting mathematical questions, but not obviously so. (How's that for a resume bullet!) I've already touched on why I think non-obviousness is important, but there's another reason: when the contextual link is trivial, the question generally becomes terrible. And it's really, really easy to create trivial links. And then the real-world problem is no longer isomorphic; rather it becomes both substantially identical to and superficially uglier than the original problem, which is unproductive. It's easy to pour a thin candy shell of context that does nothing to conceal the shape of the underlying problem, or to improve its flavor. The real world can definitely ruin a task if your only goal is to incorporate something --- anything --- non-mathematical because for some reason you're afraid to ask a math question about math.
And in that sense I understand the impetus behind the 'fake-world math' backlash, because there's a certain amount of extant conviction that slapping the 'real-world' label on something magically confers awesomeness...which it certainly does not. Such wanton slapping can also make it seem as though it's somehow desirable to avoid mentioning mathematics while teaching it, which is a lousy way to treat of such a rich subject, and rather unsubtly suggests that math is unpalatable on its own. We should, as a community, take the position that a poorly executed idea ought to be avoided. We should question the circumstances and mechanisms that lead to poor execution. I also think we shouldn't dismiss the good idea outright. The real world isn't a silver bullet, but it's a perfectly good bullet to have in the magazine.
P vs. NP
I mentioned supra that, while I find this question of to be intellectually interesting, I don't think it's especially important. Mostly because what I'm interested in, globally, are great math tasks, and the greatness of a task is independent of whether it's situated in- or outside of the real world, however we choose to limn it. There is only the illusion of dichotomy here. I drew my own personal line, and I chose to work on one side of it because I'm partial to the view from over here. But I also realize that the work I do at Mathalicious represents a small (though valuable) part of the mathematical experience students should have.
I think that work like mine and work like Dan's approach the same target from essentially opposite directions. Dan is trying to reify mathematics by treating it as a properly first-class citizen in the world as we know it. I'm trying to expand mathematical thinking to comprise those parts of the world we may not realize are already within its purview. Somewhere in the middle we create a situation in which mathematics and the real world end up occupying essentially the same space. Isn't that what we're all doing? I hope so. I'd really like that world.