As happens with amazing frequency, Christopher Danielson said something interesting today on Twitter.
Dear children's publishing industry: It is NOT a property of rectangles that they have "two long sides and two short sides". #ThatIsAll
— Christopher (@Trianglemancsd) July 29, 2013
— Christopher (@Trianglemancsd) July 29, 2013
And, as also happens with impressive regularity, Max Ray chimed in with something that led to an interesting conversation --- which, in the end, culminated in my assertion that not everything that is mathematically true is pedagogically useful. I would go further and say that a truth's usefulness is a function of the cognitive level at which it becomes both comprehensible and important --- but not before.
By way of an example, Cal Armstrong took a shot at me (c.f. the Storify link above) for my #TMC13 assertion that it is completely defensible to say that a triangle (plus its interior) is a cone. Because he is Canadian, I think he will find the following sentiment particularly agreeable: we're both right. A triangle both is, and is not, a cone, depending on the context. It might be helpful to think of it as Schrödinger's Coneangle: an object that exists as the superposition of two states (cone and triangle), collapsing into a particular state only when we make a measurement. In this case, the "measurement" is actually made by our audience.
When I am speaking to an audience of relative mathematical maturity, I can (ahem...correctly) say that cone-ness is a very broadly defined property: given any topological space, X, we can build a cone over X by forming the quotient space
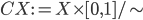
with the equivalence relation ~ defined as follows:
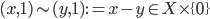
If we take X to be the unit interval with the standard topology, we get a perfectly respectable Euclidean triangle (and its interior). Intuitively, you can think of taking the Cartesian product of the interval with itself, which gives you a filled-in unit square, and then identifying one of the edges with a single point. Boom, coneangle. Which, like Sharknado, poses no logical problems.
Of course, it is a problem when you're talking to a middle school geometry student. In that situation, saying that a triangle is a cone is both supremely unhelpful and ultimately dishonest. What we really mean is that, in the particular domain of 3-dimensional Euclidean geometry, when we have a circle (disk) in a plane and one non-coplanar point, we can make this thing called a cone by taking all the line segments between the point and the base. But to that student, in that phase of mathematical life, the particular domain is the only domain, and so we rightly omit the details. In an eighth-grade geometry class, there is absolutely no good reason to introduce anything else.
We do this all the time as math teachers. "Here, kid, is something that you can wrap your head around. It will serve you quite well for a while. Eventually we're going to admit that we weren't telling you the whole story --- maybe we were even lying a little bit --- but we'll refine the picture when you're ready. Promise."
Which brings me back to Danielson's tweet. From a mathematical point of view, there are all kinds of problems with saying that a rectangle has "two long sides and two short sides" (so many that I won't even attempt to name them). But how bad is this lie? Better yet, how bad is the spirit of this lie? I think it depends on the audience. I'm not sure it's so very wrong to draw a sharp (albeit technically imaginary) distinction for young children between squares and rectangles that are not squares. It doesn't seem all that different to me, on a fundamental level, from saying that cones are 3-dimensional solids. Or that you can't take the square root of a negative number. Or that the sum of the interior angles of a quadrilateral is 360 degrees. None of those statements is strictly true, but the truths are so very inconvenient for learners grappling with the concepts that we actually care about at the time. It's not currently important that they grasp the complete picture. And it's probably not feasible for them to do so, anyway.
Teaching mathematics is an iterative process, a feedback loop. New information is encountered, reconciled with existing knowledge, and ultimately assimilated into a more complete understanding. Today you will "know" that squares and rectangles are different. Later, when you're ready to think about angle measure and congruence, you will learn that they are sometimes the same. Today you will "know" that a times b can only be 0 if either a or b is zero. And tomorrow you will learn about the ring of integers modulo 6.
I will tell you the truth, children. But maybe not today.

I think the bigger pushback among people I talked to was the assertion that pyramids are a subset of cones. I argued that it was probably related to the discussion of whether circles are polygons. If so, then I agree with how you. If not, then, in my head, cones have circular bases while pyramids have polygonal ones.
That's another great example. All pyramids are cones, but not all cones are pyramids (regardless of a circle's status as a polygon). If you let X be some polygonal region of the Euclidean plane, the construction above will still give you a topological cone. In fact, in 3D Euclidean space (to say nothing of the more general case), all geometric cones are isomorphic.
You can go much further. There's nothing saying that X has to be a Euclidean space. It can be any topological space at all. Which of course means that you can have a perfectly well-behaved and well-defined cone that you can't even visualize...because it's not made of geometric points/lines/segments/rays!
Thanks for writing this. I am 100% enamored with "a truth’s usefulness is a function of the cognitive level at which it becomes both comprehensible and important — but not before." Now I'm wondering if that's a definition of usefulness, and if we could play the "What is..." game. But that's for later. For now I wanted to think about squares and rectangles and assessing comprehensability and import.
At first I was musing on fruit and strawberries. Even young kids understand that strawberries are fruit and not all fruit are strawberries (sadly). Then I wondered if kids saw more groups labeled as "rectangles" that included square rectangles, if they would have less trouble understanding the relationship between squares and rectangles. Then I wondered if kids got to sort quadrilaterals and label their own categories, if they would have an easier time with the square/rectangle relationship, and if so, show us that they are ready to comprehend the relationship because it's important to their sorting.
But in thinking about how a good sorter might sort squares and rectangles, I think she'd be likely to have a big category of "right angle corners" and two subcategories of "all sides equal" and "two pairs of opposite sides equal". The big piece that novice math definers would struggle with is not that squares participate in larger categories but that the larger category in some sense is sharing a name with its own more general subcategory (I know that's not AT ALL how a mathematician would think of that, but it is how I think a learner would think of it).
I wonder if there's more hard, fun work to be done in diagnosing what the hard parts of the big lies are so that we can be aware of them and make elementary and secondary mathematics more robust? For example, would it be easier for kids to learn to identify all right-angled quadrilaterals as rectangles and then sort rectangles into squares and long-shorts? And later on to learn there's no reason to call long-shorts anything other than rectangles? (Then what happens to rhombuses, and knowing that a square is also a rhombus... this stuff is tricky!)
As a lover of both strawberries and sorting activities in the classroom, I'm intrigued by this idea.
In musing on fruits, I'm beginning to think they present an amazing metaphor. When you're a child, you are presented with all of these foodstuffs, and so you begin to classify them according to certain properties. At the very coarsest level, you have a plant-based category (fruigetables), which then gets subdivided into sweet/delicious and savory/gross, which roughly correspond to fruits and vegetables, respectively. You get older, and you refine your categories as you gain new information, but you always retain some elements of your earliest impressions --- and sometimes that leads to confusion and mistakes. (A cucumber is a fruit? Really, science?) But when you're first learning about fruits, some of those subtle distinctions aren't important. After all, if you can identify something as coming from a plant rather than from an animal, that's a pretty important step in your culinary development. Also, you don't have the cognitive tools to make a truly rigorous distinction. You can't do that until you know something about ovaries and endosperms and plant tissues, which is something you can get around to later, more or less as an afterthought (literally), because the naming is so much less important than the culinary properties in most instances.
I'm imagining that a kid learning what a rectangle looks like relative to a square is something akin to a kid learning what fruit looks like relative to a strawberry. Strawberries have some things in common with all fruits, but also some things that are uniquely strawberry-y. It is not entirely wrong to say that strawberries behave in a certain way, and fruits behave in a certain, different way, even though a strawberry must, by definition, behave in a fruitlike way! Homing in, ever more precisely, on what makes a strawberry a non-cherry will take a lot of climbing up the cognitive ladder. There will be new concepts, new vocabulary to give voice to those concepts, &c. But I think a good first step is noticing the similarities and differences, even if we point out subtly false distinctions (and I would argue that, to a nontrivial age range of children, whether or not an all-right-angle quadrilateral has congruent sides is subtle).
Eventually, a kid will get to a point where she can make nuanced observations about the relationship between rhombuses and squares and rectangles and parallelograms, just like a sufficiently thoughtful adult can say that wheat is technically a fruit (but with a very thin fruit wall and a prominent seed), and a walnut (which looks an awful lot like a seed) is really more closely related to a tomato than a sunflower seed...but that's a long way off. I'm okay starting with little lies.
This post reminded me of two things. First, the Devin-centered "multiplication is not repeated addition" debate, and whether it's ever okay to teach it that way. Second, some examples from Becker & Jacob's (2000) PDK article about anti-reformers in California's math wars in the late '90s. I find these amusing/frustrating, so I'll quote the article at length here:
The beliefs of mathematicians about problem solving and conceptual understanding are illustrated through their discussions of inappropriate curricula. In the framework, a mathematician author wrote the following about a kindergarten problem:
We must remember that this is a discussion about teaching mathematics in kindergarten! (p. 532)
I thought this story was worth quoting, too:
In the public presentation, the two mathematics professors had an opportunity to explain the overarching themes behind their revision of California policy. One discussed why extensive practice with the long division algorithm is so important. He explained that students learning differential equations at Stanford University lacked adequate proficiency with long division of polynomials, which they needed for their Laplace transform functions. Apparently this difficulty is the fault of their elementary teachers, who, when these Stanford students were in their classrooms, would have used the same parrot math California has now resuscitated. Later, the importance of proof in grade 7 as preparation for algebra was emphasized. For example, the other professor rigorously proved that (-2/5) x (7/4) = -[(2/5) x (7/4)]. The identical proof was repeated a second and third time in response to questions from the audience. After his second time through, some members of the audience were not convinced, and the professor remarked, "I'm puzzled as to why this is difficult. I'm not trying to make fun of you." In this way publishers learned why formal reasoning across the grades is so essential to marketing their products in California. (p. 532)
There is certainly a time for precision, but that can't mean it's always time for precision, whether its in learning math or something else. We've found wonderful ways to structure mathematics, but that doesn't mean the learning of mathematics follows the same structure.
Becker, J. P., & Jacob, B. (2000). The politics of California school mathematics: The anti-reform of 1997-99. Phi Delta Kappan, 81(7), 529–537.
I agree with your general point about precision having a time and place. And, in that vein, the spirit of SMP.6 applies to teaching as well as learning mathematics. Also, I like your distinction between the way we structure mathematics and the way we present that structure, which is incredibly important. I often find myself in a similar debate about teaching math through historical perspectives; i.e., the way mathematics actually developed (temporally) isn't always pedagogically useful. Unfortunately for us, people didn't discover things in a way that is linearly appropriate for teaching all this messily-aggregated knowledge. Hence our job is harder.
I have to say, in the interest of full disclosure, that I'm in the pro-Devlin camp w/r/t multiplication not being repeated addition. But not because I disagree with your main premise (that complete mathematical rigor shouldn't be placed above effective teaching/learning progressions). In the particular case of multiplication, it turns out that the mathematical rigor part and the pedagogy soundness part have some real overlap. I'm too lazy to dig up references (kudos to you, by the way), but there is evidence (some of which is nicely organized by NCTM in their stuff on proportional reasoning) that thinking of e.g., 3 inches as the sum of three one-inch units rather than a standard one-inch unit scaled by a factor of 3, does more harm than good in terms of developing reasoning about multiplicative relationships in the context of proportions. It's a healthy debate to keep having, and I know Danielson will probably read this and come down on your side in further comments. Thanks for the input.
Pingback: Consider the Strawberry | Lines and Lines of Tangency
And he's back!
I love, "... how bad is the spirit of this lie?" In the classroom, sometimes the whole truth is just too much to know at that moment. Doesn't mean we have to go all Colonel Jessup/Code Red on kids, but we may have to wait a bit while their thinking process catches up with the truths of a concept.
Well done.
Since math ed is becoming so structured, it would behoove the community to agree upon the pragmatic and age appropriate fibs, and when and how to reveal them. It even makes sense to do multiple fibs, eventually relying upon future teachers to clarify. Little hints are good, a peek behind the curtain. But it's better to lie to students about what mathematics is until they have the psychological development to appreciate it. Like sausages. Or Santa.