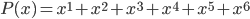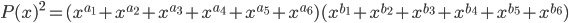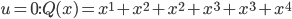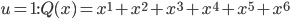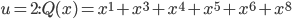There's an interesting article in this month's Mathematics Teacher about the effects of the particular language elements we use to communicate mathematical ideas. The main thread revolves around limit concepts, primarily because they're both philosophically and practically confusing for many beginning calculus students, and because, it turns out, a teacher's particular choices regarding words and metaphors have an important impact on student (mis)understanding.
Limits comprise a special relationship between mathematical process and mathematical object. We speak of them in terms of variables "approaching" or "tending toward" particular values, but we subsequently manipulate them as static entities. I can, for instance, talk about the limiting value of the expression 1/x as x grows without bound (a dynamic concept), but that limiting value is ultimately just a single real (static) number: zero. There's an uncomfortable tension in that duality.
Even the notation is ambiguous. Here's the fact I mentioned in the preceding paragraph, symbolically:

The arrow implies motion, but the equals sign implies assignment. There are elements of both process and object.
I've touched on this duality before, which has sparked some great conversations. A few months ago, I had a supremely interesting email chat with Christopher Danielson after he pointed me toward the writings of Anna Sfard. He has graciously agreed to allow me to reproduce that conversation here in its original form; I've only redacted some of the more boring pleasantries and collapsed some strings of shorter messages into longer ones. Enjoy.
Chris Lusto
To: Christopher Danielson
Seriously, thanks for the Sfard tip. I've read a few of the articles she has on her website (which, by the way, why are college professors' websites like the most aesthetically displeasing things on the internet? Just use a white background and stop being weird.), and you were right: I dig her. I read the article on duality [PDF] and had one major bone of contention.
I really like the idea of duality versus dichotomy, and she makes, I think, a compelling argument in general. I just worry it might just be a little ambitious. She hedges a little bit, saying things like "more often than not" mathematical objects can be conceived both operationally and structurally, but I still think this idea of duality runs into serious problems when infinite things come into play--and that's not exactly a trivial subset of "mathematical objects."
If we allow that operational conception is (a) just as valid/important as structural and (b) often, in fact, precedes structural conception, what are we to make of processes that never end, that never produce anything because they're always in production? Sfard even says, "...interpreting a notion as a process implies regarding it as a potential rather than actual entity, which comes into existence upon request in a sequence of actions." But what if we can't ever fulfill the request, because we're always on hold, waiting in vain for the end of an unending sequence? And what about this business of "potential?" That just smacks of the "potential infinities" of the ancient Greeks that held back western mathematics for a couple millennia. It seems like we have to admit either (a) an infinite process can terminate in finite time in order to produce an structural object, or (b) these objects aren't really at all structural, because they live in the world of potentiality. I don't find either of those particularly satisfying. I think, in the case of infinite notions, the operational conception leads to a fundamental misconception, a la my student D.
Your thoughts? Whenever you have a moment, of course.
Chris
Christopher Danielson
To: Chris Lusto
"Ambitious" describes Anna Sfard's intellectual habits very well, I think. She was in a half-time appointment at Michigan State (and half time at Haifa) for part of my grad school time, and she was on my dissertation committee. The woman is crazy smart. And it seems to be a characteristic of Israeli intellectuals to commit very strongly to one's ideas. Not a maybe or a perhaps to be found in her oeuvre, I don't think.
I have no explanation for the poor poor quality of academics' websites, except to say that it is representative of tech use in higher ed more generally. See also @EDTECHHULK on Twitter and Dan Meyer's comments here (esp. couple screens down the page, at "Real Talk about Grad School):
http://blog.mrmeyer.com/?p=12592
I'm still formulating thoughts on processes that never terminate. But I'm not sure I fully understand your objection. Your classroom scenarios seem to suggest that indeed process and object are both fundamentally important ways of thinking about infinity. And consider the language of limits..."as x goes to infinity" or even "as x grows without bound". Those are both process-based ways of talking, right?
csd
Chris Lusto
To: Christopher Danielson
I think Sfard's right that, in general, process and object are both important methods of mathematical conception. And yeah, multiple representations are not only admissible, but probably desirable (thinking here, specifically, of HS algebra and the Lesh Model), but isn't operational understanding misleading when you're talking about infinity?
Thinking of f(x) = 2x as a process that doubles inputs is valuable, and so is a picture of the resulting object/graph. And, in a case like this one, I don't think you lose or gain all that much with either vantage. Sometimes it's helpful to think of the process, and other times the object.
But thinking of asymptotic behavior procedurally, for example, is very, very different from the object we call a "limit." It's nice if students can understand that, as x gets larger, 1/x gets arbitrarily close to 0. I mean, certainly if we hold a numerator constant and increase the denominator, this process yields subsequently smaller and smaller values. But I think that's still like a mile away from understanding that lim_x-->∞ {1/x} = 0. Like, is equal to. Is identical to as an object. Is just another name for. Like, 23 + lim_x-->∞ {1/x} = 23.
If procedure (process) is linked to product (object)--like, say, "4 divided by 7" is linked to "4/7"--then how are we to reconcile a never-ending process with a finite, tangible product that can be manipulated like any other mathematical object? Doesn't it force us to accept that 1/x eventually "gets to" 0 (which it doesn't), or that the limit is some kind of potential result (which it isn't) that can't really ever be called a proper object because the process is, by definition, never-ending?
I'm going to stop typing words, because I feel like as my words -->∞, my clarity --> 0.
C
Christopher Danielson
To: Chris Lusto
I see...so to boil it down to a debatable question...
Is the object necessarily the product of the process?
Do I have it right?
btw...if I got that question right, then I say 'no'.
I can think about 1,352,417 and treat it as an object, even though I can assure that I have never participated in any sort of process that yielded that number.
To say nothing of googolplex.
csd
Chris Lusto
To: Christopher Danielson
I think that's about right, but with one important qualification.
Is the object necessarily the product of the process? Then I agree, no. But you at least have the option of defining it either way. Even if you've never constructed 1,352,417 widgets, there's nothing philosophically problematic with the process that did/could. You're right, there isn't even a measly googol of anything, but that doesn't stop it from being the eventual result of (1+1+...+1).
So...
Is the object the result of the process? Not necessarily, but that's not a huge problem for me.
Could the object be the result of the process? If the answer is no (which my gut believes it to be in the infinite case), then how can we reasonably talk about it as both a process and an object? Does the duality break down?
C
Christopher Danielson
To: Chris Lusto
See I don't see a huge difference philosophically between "a product that could be created by a known process, but not in my lifetime" (counting to googol) and "a product that could never be created" (infinity).
In both cases, for me, the process is (1) incomplete, and (2) hypothetical.
Why does it matter at the core whether the result is theoretically achievable or not? Either way, I've imagined it.
And I think imagination is key. I don't recall whether Sfard writes about that or not (probably not, since she's all language, no imagery). But I do think the transition from process to object is at least in part one involving imagination. I have to imagine the object into being in mathematics precisely because mathematical objects are abstract.
And when I'm struggling to understand a new object (say a limit), it is often helpful to imagine the process that produced it. But I don't have to see the process through to the end.
csd
Chris Lusto
To: Christopher Danielson
Think about our Hz conversation. Even with arbitrarily huge numbers of wave combinations, we get sinusoidal waves. I can get as close to a square wave as I want, but in order to actually obtain the square wave object, the process that got me arbitrarily close to my goal breaks down and fails. The process is insufficient to the object. The difference between the square wave and the sinusoidal wave that's arbitrarily close to square is ultimately qualitative, not just quantitative--and there's the rub. Wasn't that precisely what you and Frank [Noschese] convinced me of?
C
Christopher Danielson
To: Chris Lusto
But the square wave is the limit. There's the object. The limit (process? object?) produces the square wave.
I have no idea what I convinced you of. But I know that the argument I was making was that polynomials-by definition-have finitely many terms. And e^x can be written as infinitely many terms, each one a polynomial. Is e^x a polynomial? By the letter of the law, no. But in spirit? Yes. And that's beautiful.
I got in trouble doing a CMP demonstration lesson once. I talked with students about a cylinder being a circular prism. The algebra teacher observing got upset with me because a prism has polygonal faces. Ergo, "circular prism" is nonsense.
I had occasion to follow up a year or so later with my former complex analysis professor from MSU grad school. He had absolutely no problem calling a cylinder a circular prism. No problem at all.
What to learn? Unclear.
csd
Chris Lusto
To: Christopher Danielson
I see a huge distinction between "unachievable due to resource constraints" and "unachievable by definition." Why is the possibility that CERN moved some particles faster than light a big deal? We've already moved all kinds of stuff 99.999999% that fast in the lab. The extra .000001% is practically trivial, but philosophically enormous. It's not that faster-than-light travel seemed to be practically impossible, but literally, probability exactly 0 impossible.
The difference between almost 0 and 0, no matter how small, is mathematically gigantic.
This is seriously all kinds of fun, but I have to go do some domestic things. To be continued...in finite time.
C
Christopher Danielson
To: Chris Lusto
That's the beautiful thing about email. It is at heart an asynchronous medium.
By the way, some would say that you have pointed to an important difference between mathematics and the sciences with your example.
csd
Thanks so much to Dr. Danielson for (a) having this discussion, and (b) letting me publish all the gory details. Oh, and (c) making me smarter in the process.